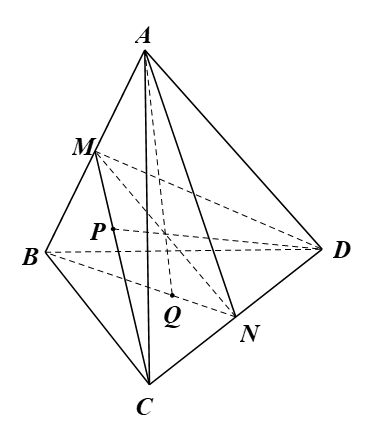
Trọng tâm của tứ diện
I. Lý thuyết
1. Định nghĩa
Điểm G trong các công việc bên trên được gọi là trọng tâm của tứ diện ABCD.
Ta rất có thể nói: Trọng tâm của một tứ diện là trung điểm của đoạn nối những trung điểm của cặp cạnh đối lập.
2. Tính chất

II. Ví dụ minh họa
Ví dụ 1: Giả sử tứ diện ABCD với trọng tâm G và tứ diện A'B'C'D' với trọng tâm G'.
Hướng dẫn giải
Ta cần thiết minh chứng rằng nếu như vector AA' → + BB' → + CC' → + DD' → = 0, thì G cũng chính là trọng tâm của tứ diện A'B'C'D'.
=> Ta màn biểu diễn vector AA' → + BB' → + CC' → + DD' → vì chưng tổng những vector kể từ G cho tới những đỉnh:
AA' → + BB' → + CC' → + DD' → = (AG' → + GG' →) + (BG' → + GG' →) + (CG' → + GG' →) + (DG' → + GG' →) = AG' → + BG' → + CG' → + DG' → + 4GG'
→.Vì vector AA' → + BB' → + CC' → + DD' → = 0, tớ có:
AG' → + BG' → + CG' → + DG' → + 4GG' → = 0.
Suy ra: AG' → + BG' → + CG' → + DG' → = -4GG' →.
Nhưng theo đuổi khái niệm, G là trọng tâm của tứ diện ABCD tức là AG → + BG → + CG → + DG → = 0.
Do bại, tớ có:
AG' → + BG' → + CG' → + DG' → = AG' → + BG' → + CG' → + DG' → + 4GG' → + 4(G → - G →) = AG' → + BG' → + CG' → + DG' → + 4(G → - G →) = (AG' → + BG' → + CG' → + DG' → + 4G →) - 4G → = 0 - 4G → = -4G →. Từ bại suy rời khỏi -4G → = -4GG' →, hoặc G → = GG'
→.Vậy, nếu như vector AA' → + BB' → + CC' → + DD' → = 0, thì G cũng chính là trọng tâm của tứ diện A'B'C'D'.
Điều ngược lại cũng tương tự động, tớ rất có thể minh chứng rằng nếu như G cũng chính là trọng tâm của tứ diện A'B'C'D', thì vector AA' → + BB' → + CC' → + DD' → = 0.
Vậy, tớ đang được minh chứng được rằng G cũng chính là trọng tâm của tứ diện A'B'C'D' khi và chỉ khi vector AA' → + BB' → + CC' → + DD' → = 0.
Ví dụ 2: Cho tứ diện ABCD. Gọi M, N, P.., Q, R, S theo thứ tự là trung điểm của những đoạn trực tiếp AC, BD, AB, CD, AD, BC. Chứng minh rằng những đoạn trực tiếp MN, PQ, RS đồng quy bên trên trung điểm G của từng đoạn.
Hướng dẫn giải
Trong tam giác ACD tớ với MR là đàng tầm nên (1)
Tương tự động tam giác BCD, tớ với (2)
Từ (1) và (2), tớ suy rời khỏi
Dó bại tứ giác MRNS là hình bình hành. Như vậy MN, RS rời nhau bên trên trung điểm G của từng đoạn
Lí luận tương tự động tớ với tứ giác PRQA là hình bình hành nên PQ, RS rời nhau bên trên trung điểm G của từng đoạn. Vậy PQ, RS, MN đồng quy bên trên trung điểm của từng đoạn
III. Bài luyện vận dụng
Bài 1: Chứng minh điểm G là trọng tâm của tứ diện ABCD khi và chỉ khi một trong những nhị ĐK xảy ra:
a)
b) với từng điểm P
Giải
Gọi M, N theo thứ tự là trung điểm của đoạn AB, CD
a) Ta với
Điểm G là trọng tâm của tứ diện ABCD khi và chỉ khi
Điều này tương tự với
b) G là trọng tâm của tứ diện ABCD khi và chỉ khi
Điều này Có nghĩa là với điểm P.. bất kì, tớ có:
hay
Bài 2: Gọi G là trọng tâm tứ giác ABCD
a) Chứng minh rằng đường thẳng liền mạch trải qua G và một đỉnh của tứ diện tiếp tục trải qua trọng tâm của mặt mày đối lập với đỉnh ấy
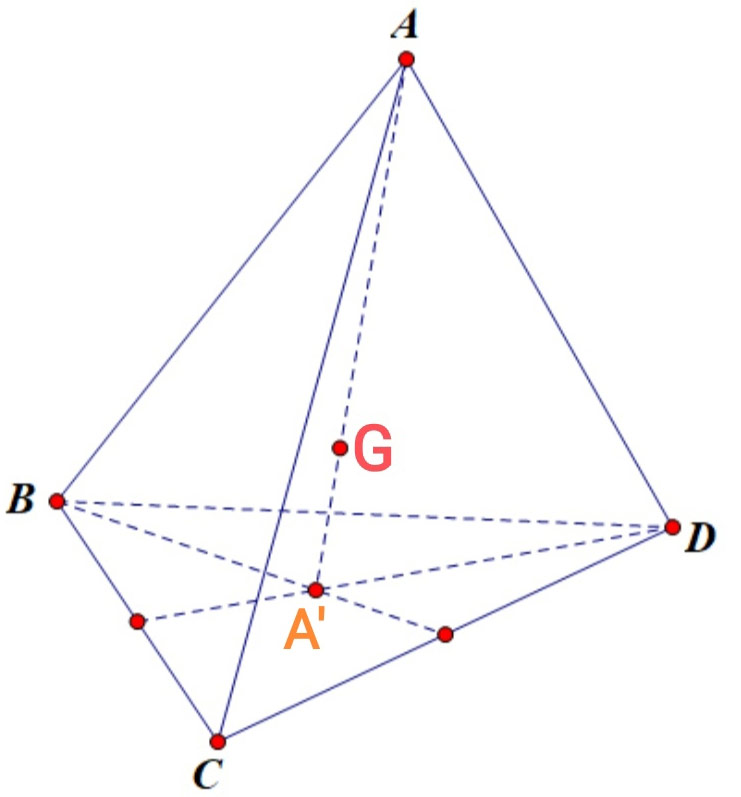
b) Gọi A' là trọng tâm của mặt mày BCD. Chứng minh rằng GA = 3GA'
Giải:
Gọi P.., Q theo thứ tự là trung điểm cuae AB và CD thì trọng tâm G của tứ diện ABCD là trung điểm của PQ.
Giả sử đường thẳng liền mạch AG rời mp(BCD) bên trên A'. Ta cần minh chứng A' là trọng tâm tam giác BCD. Rõ ràng A' nằm trong đàng trung tuyến BQ của tam giác BCD. Từ P.. tớ kẻ PP'//AA' thì PP' là đàng tầm của tam giác ABA'. Còn GA' là đàng tầm của tam giác QPP', tức là BP' = P'A' = A'Q(*) và AA' = 2PP', PP' = 3GA'(**)
a) Từ (*) suy rời khỏi A' là trọng tâm tam giác BCD
b) Từ (**) suy rời khỏi AA' = 4GA' hoặc GA = 3GA'
Bài 3: Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
Giải:
Theo quy tắc 3 điểm tớ với :
Mà G là trọng tâm của tam giác ABC nên:
Từ (1) và (2) tớ có:
Bài 4: Cho tứ diện ABCD với P.., Q theo thứ tự là trọng tâm của tam giác ABC và BCD. Giao tuyến của mặt mày phẳng phiu (ABQ) và mặt mày phẳng phiu (DCP) là đường thẳng liền mạch d. Khẳng quyết định này tiếp sau đây đúng?
A. d trải qua trung điểm nhị cạnh AB và CD.
B. d trải qua trung điểm nhị cạnh AB và AD.
C. d là đường thẳng liền mạch PQ.
D. d là đường thẳng liền mạch QA.
Lời giải:
Đáp án đích thị là: A
Gọi M, N theo thứ tự là trung điểm của AB, CD.
Ta với M ∈ AB nhưng mà AB ⊂ (ABQ), nên M ∈ (ABQ) (1)
Khi bại đàng trung tuyến CM trải qua trọng tâm P.. của của ∆ABC.
Do bại mặt mày phẳng phiu (DCP) đó là mặt mày phẳng phiu (DCM), nên M ∈ (DCP) (2)
Từ (1) và (2) suy rời khỏi M ∈ (ABQ) ∩ (DCP).
Tương tự động tớ cũng có thể có N ∈ (ABQ) ∩ (DCP).
Suy rời khỏi (ABQ) ∩ (DCP) = MN.
Bài 5: Gọi G là trọng tâm của tứ diện ABCD. A’ là trọng tâm của tam giác BCD. Tính tỉ số GA/GA’ là:
Giải
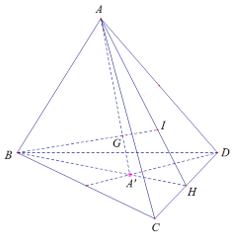
Gọi I là trọng tâm tam giác ACD
H là trung điểm CD
Nối BI rời AA’, tớ được trọng tâm G của tứ diện
Xét mặt mày phẳng phiu (ABH)
Ta có:
( A’ và I theo thứ tự là trọng tâm những tam giác BCD và ACD)
A’I // AB
Ta lại có: ( vận dụng quyết định lý tớ lét)
GA = 3GA’